K-means voor auditors: clustering & outliers

K-means clustering is een krachtige techniek om patronen en afwijkingen in data te ontdekken, maar wordt binnen de audit nog maar beperkt gebruikt. In dit artikel leggen we uit wat het is en hoe je het wél en niet kunt inzetten.

In de context van auditing biedt deze methode twee belangrijke mogelijkheden:

1. Transacties groeperen op basis van kenmerken
2. Outliers identificeren die mogelijk wijzen op fouten of fraude

In dit artikel richten we ons vooral op het tweede doel: het opsporen van outliers in grootboektransacties. Maar eerst geven we een overzicht van de algemene toepassingsmogelijkheden.

Wat is K-means clustering?

K-means is een unsupervised machine learning-algoritme dat data verdeelt in k groepen (clusters) op basis van hun onderlinge afstand. Het doel is om binnen een cluster zoveel mogelijk gelijkenis te hebben en tussen clusters zoveel mogelijk verschil.

Waarom relevant voor de audit?

Voor auditors kan het analyseren van duizenden of zelfs miljoenen transacties overweldigend zijn. K-means clustering biedt hierbij ondersteuning door structuur aan te brengen in complexe datasets. Door transacties te groeperen op basis van vergelijkbare kenmerken kunnen auditors sneller inzicht krijgen in typische patronen en gedragingen binnen financiële processen. Wanneer bepaalde transacties sterk afwijken van deze patronen — bijvoorbeeld qua bedrag, tijdstip of combinatie van kenmerken — kunnen deze als outliers worden gemarkeerd. Dit kan je helpen om je aandacht te richten op potentieel risicovolle of foutieve boekingen.

Clustering ondersteunt dus niet alleen bij fraudedetectie, maar ook bij risicogerichte planning, het trekken van steekproeven en het verbeteren van het procesbegrip. Het draagt bij aan een efficiëntere en effectievere controleaanpak.

Voorbeeld: grootboektransacties analyseren

Stel, je hebt een dataset met grootboektransacties en wilt controleren of er ongebruikelijke boekingen zijn. We passen K-means toe om transacties in groepen te verdelen, waarna we outliers identificeren: de boekingen die het minst goed passen in een cluster.

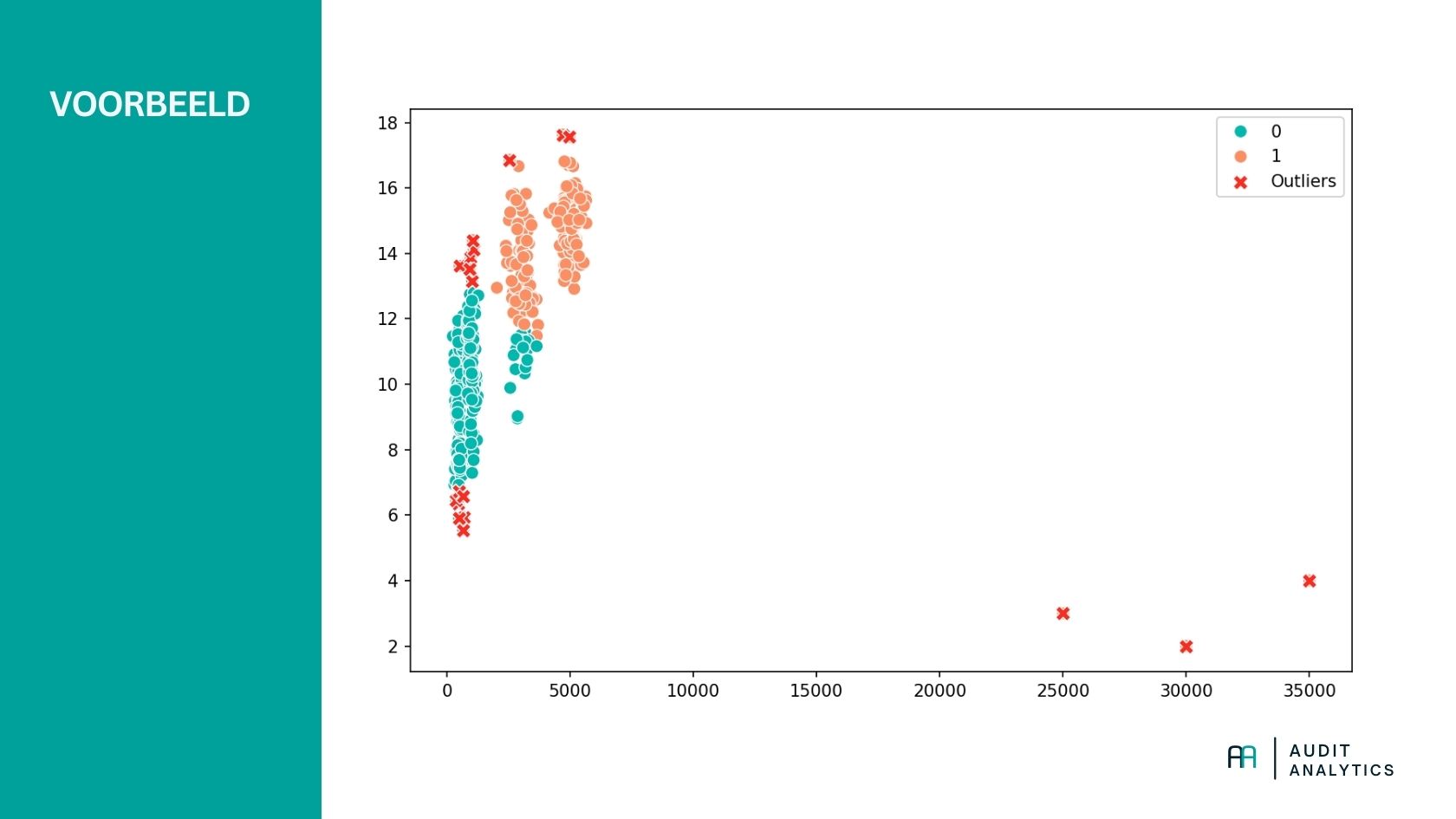
In het voorbeeld hierboven zie je dat in de dummyset een aantal boekingen zijn gemaakt van grote omvang op een ongebruikelijk tijdstip. We hebben het algoritme zo ingesteld dat we twee clusters willen zien. Alle boekingen die niet binnen een cluster passen (5% boekingen met de grootste afstand tot een clustermiddelpunt), zijn gedefinieerd als outlier.

Aantal clusters kiezen

Voordat je K-means toepast, is het belangrijk om het juiste aantal clusters (k) te bepalen. Dit bepaalt hoeveel verschillende groepen het algoritme gaat maken. In het voorbeeld hierboven zeiden we bijvoorbeeld dat we twee clusters verwachten. Echter, als we zouden zeggen dat we er vier verwachten, krijgen we het volgende:

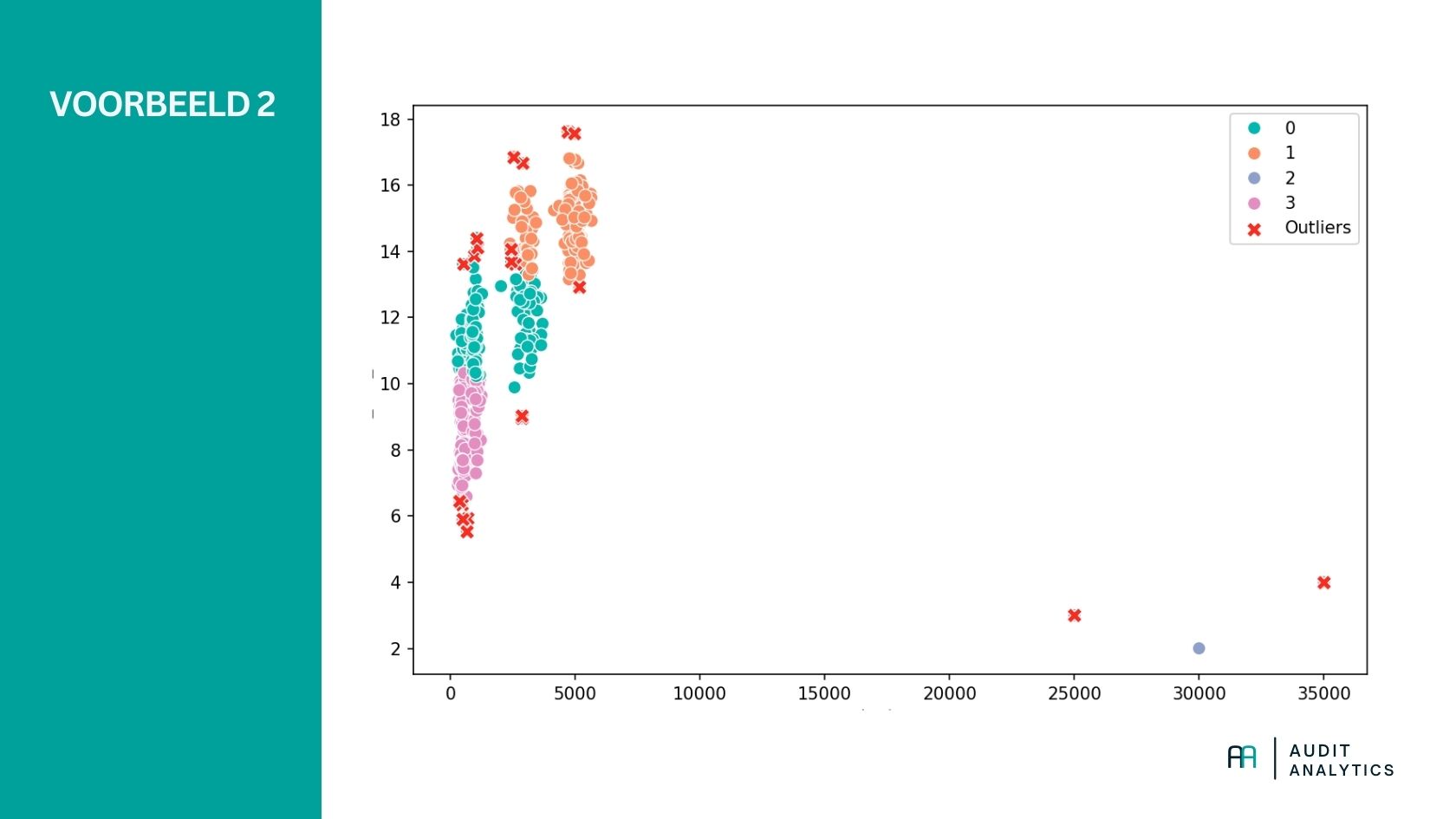
Je ziet het al: nu zijn een aantal andere outliers gedefinieerd. Dat is logisch, immers zijn er nu meerdere middelpunten. Het is dus van cruciaal belang dat je een goed aantal clusters bepaald en dit kunt verantwoorden.

Een veelgebruikte methode is de elbow-methode, waarbij je de variantie binnen de clusters uitzet tegen het aantal clusters. Het punt waarop de afname in variantie afvlakt (de 'elleboog') geeft vaak een geschikt aantal aan.

Normaliseren

Voor een goede clustering is het cruciaal dat alle variabelen op een vergelijkbare schaal liggen. Stel dat je werkt met zowel bedragen (in duizenden euro's) als tijdstippen (in uren), dan zou zonder normalisatie het algoritme vooral letten op verschillen in bedragen, omdat die schaal veel groter is. Door de data te normaliseren (standaardiseren), breng je alle variabelen naar een gelijke schaal, meestal met gemiddelde 0 en standaarddeviatie 1. Zo voorkom je dat een bepaalde variabele de clustering onbedoeld domineert.

Stap-voor-stap Python-script

We gebruiken Python met pandas, scikit-learn en matplotlib. Heb je deze packages nog niet? Installeer ze dan met pip:

pip install pandas scikit-learn matplotlib

Dit script bevat ook gesimuleerde voorbeelddata.

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import seaborn as sns

# Voorbeelddata: gesimuleerde grootboektransacties
np.random.seed(42)
data = pd.DataFrame({
    'bedrag': np.concatenate([
        np.random.normal(500, 100, 100),
        np.random.normal(1000, 100, 100),
        np.random.normal(3000, 300, 100),
        np.random.normal(5000, 300, 100),
        [25000, 30000, 35000]  # outliers
    ]),
    'uur_van_dag': np.concatenate([
        np.random.normal(9, 1.5, 100),
        np.random.normal(11, 1.5, 100),
        np.random.normal(13, 1.5, 100),
        np.random.normal(15, 1.0, 100),
        [3, 2, 4]  # outliers
    ])
})

# Normaliseren van de data
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)

# K-means clustering met 2 clusters (voorbeeld). 
# Random_state bepaalt het willekeurige startpunt. Door deze gelijk te houden, blijf je dezelfde resultaten houden. 
kmeans = KMeans(n_clusters=2, random_state=60)
data['cluster'] = kmeans.fit_predict(data_scaled)

# Afstand tot clustercentrum berekenen
data['afstand_tot_clustercentrum'] = np.linalg.norm(data_scaled - kmeans.cluster_centers_[data['cluster']], axis=1)

# Outliers: hoogste 5% op basis van afstand
threshold = data['afstand_tot_clustercentrum'].quantile(0.95)
outliers = data[data['afstand_tot_clustercentrum'] > threshold]

# Plotten
plt.figure(figsize=(10, 6))
sns.scatterplot(data=data, x='bedrag', y='uur_van_dag', hue='cluster', palette='Set2', s=60)
sns.scatterplot(data=outliers, x='bedrag', y='uur_van_dag', color='red', label='Outliers', s=80, marker='X')
plt.title('K-means clustering van grootboektransacties')
plt.legend()
plt.show()

Interpretatie:

• De kleuren geven de clusters weer. Vergelijkbare transacties zitten in dezelfde groep.
• De rode X'en zijn transacties die ver van hun clustercentrum liggen en dus opvallend zijn.
• Deze outliers kunnen onderwerp zijn van verdere auditinspectie.

Wanneer is K-means minder geschikt?

Hoewel K-means een nuttige techniek is, zijn er situaties waarin het minder goed werkt. K-means veronderstelt dat clusters ongeveer even groot zijn, en dat alle variabelen gelijk bijdragen aan de afstandsberekening. Als de werkelijke clusters sterk verschillen in grootte of vorm, of als er veel ruis in de data zit, kan K-means verkeerde groeperingen maken. Ook bij categorische variabelen of niet-lineaire structuren is K-means niet ideaal. Bereid je dataset dus goed voor, wanneer je dit wil inzetten.

Hopelijk heb je nu een goede introductie gekregen over hoe je K-means kunt inzetten binnen de audit. We hebben in dit artikel vooral gefocust op outliers, maar je kunt bijvoorbeeld ook kijken hoe klantgroepen bijvoorbeeld gedefinieerd kunnen worden op basis van de data.