
Benford's Law (soms ook de 'First-Digit Law' genoemd) stelt dat in veel natuurlijke datasets getallen die beginnen met een laag eerste cijfer (bijvoorbeeld 1 of 2) aanzienlijk vaker voorkomen dan getallen die beginnen met 8 of 9. Dit lijkt gek, omdat we geneigd zijn te denken dat de getallen gelijkmatig verdeeld zouden moeten zijn. In werkelijkheid blijkt dat niet zo: een getal dat begint met 1 heeft ongeveer 30% kans om voor te komen, terwijl slechts 4% à 5% van de waarden met een 9 begint.
Voor een auditor is dat een interessante conclusie, omdat afwijkingen van dit patroon soms kunnen wijzen op kunstmatige manipulatie, afgeronde of verzonnen bedragen, onlogische prijsstellingen of administratieve interventies. Benford's Law wordt daarom niet gebruikt als auditbewijs, maar als screeningtool die helpt om te bepalen waar extra controle-inspanningen zinvol zouden kunnen zijn.
De theorie in het kort
Onder Benford's Law hoort elk eerste cijfer een bekende kansverdeling te volgen. De verdeling van de eerste cijfers ziet er als volgt uit:
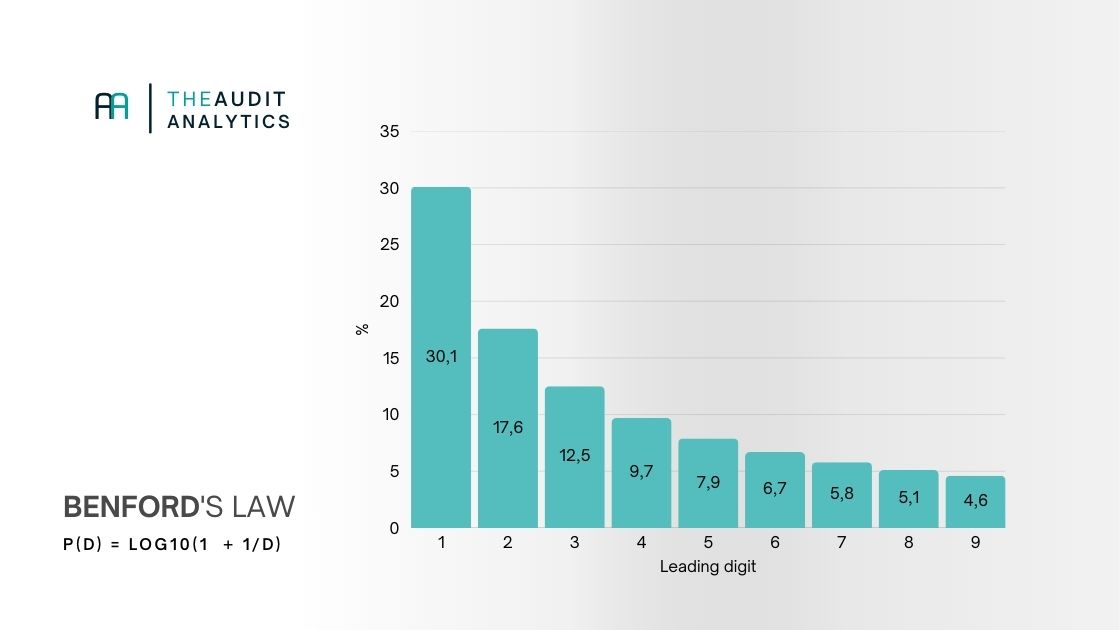
Deze percentages zijn logaritmisch bepaald: de kans dat een getal begint met cijfer d is log10(1 + 1/d). De wetmatigheid is onderbouwd door Theodore P. Hill in zijn paper "A Statistical Derivation of the Significant-Digit Law" (1995), waarin hij laat zien dat Benford-verdelingen spontaan ontstaan wanneer data uit verschillende bronnen en grootheden worden gecombineerd.
Welke data?
Voor Benford's Law kun je niet zomaar elke dataset gebruiken. De methode werkt vooral goed wanneer je beschikt over een grote hoeveelheid transacties (denk aan honderden tot duizenden facturen, declaraties of journaalposten) zodat er voldoende datapuntjes zijn om een statistisch patroon te herkennen. Daarnaast moet de data breed verspreid zijn: bedragen die variëren van bijvoorbeeld €12 tot €18.000 of zelfs hoger. Zulke natuurlijke, ongecontroleerde variatie zorgt ervoor dat de logaritmische verdeling van Benford zichtbaar kan worden.

Daartegenover staan datasets die kunstmatig begrensd zijn, bijvoorbeeld salarissen (€4950 iedere maand), declaraties die boven een limiet automatisch worden afgekeurd, of transacties die altijd net onder een drempel blijven. Ook administratieve nummering zoals factuurnummers, klantnummers of ID's is ongeschikt, omdat deze niet door economische processen ontstaan maar simpelweg volgens een systeem oplopen. Met andere woorden: Benford werkt alleen wanneer de cijfers voortkomen uit natuurlijke financiële transacties en niet door regels, processen of nummering zijn geforceerd.
Wanneer is Benford's Law zinvol in de audit?
In de auditpraktijk wordt Benford vooral gebruikt voor financiële transactiebedragen. Denk aan verkoopfacturen, inkopen, declaraties of algemene grootboekboekingen. In zulke datasets zijn bedragen zelden volledig willekeurig, maar volgen ze wel natuurlijke economische patronen.
Wanneer men facturen verzint, voorkeur heeft voor ronde bedragen of selectief bepaalde waarden kiest, is het verrassend moeilijk om intuïtief een Benford-achtige verdeling na te bootsen. Juist daardoor kan Benford afwijkingen tonen die een aanknopingspunt vormen voor nader onderzoek.
Daar tegenover staat dat Benford niet bruikbaar is voor gegevens als salarissen (vaak vaste maandbedragen), percentages, aantallen dagen, BTW-tarieven of administratieve codes. Deze waarden volgen simpelweg geen economische of natuurlijke distributie en mogen dus ook niet met Benford beoordeeld worden.
Praktisch voorbeeld in Python
Laten we het dan gaan toepassen! Hieronder gaan we aan de slag met (fictieve) declaraties van medewerkers. Het bedrijf heeft een jaar lang honderden tot duizenden declaraties ingediend, variërend van kleine uitgaven (koffie, parkeren, taxi) tot grotere posten zoals hotelovernachtingen en vliegtickets. Deze dataset is ideaal voor Benford's Law: veel transacties, natuurlijke variatie in bedragen en geen kunstmatige begrenzing.
Met onderstaande stappen voer je een eerste-cijferanalyse uit om te beoordelen of het declaratiegedrag een natuurlijk patroon volgt of dat er juist aanwijzingen zijn voor afrondingen, manipulatie of afwijkende patronen die nader onderzoek verdienen.
Data inladen en eerste significante cijfers extraheren
We beginnen met het opschonen van de declaratiebedragen en het bepalen van het eerste significante cijfer. Dit is het eerste cijfer dat er echt toe doet; dus geen voorloopnullen, valutatekens of duizendtallen.
import re
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv("jouw_dataset.csv")
# Zorg dat het bedrag numeriek is
df["Amount"] = pd.to_numeric(df["Amount"], errors="coerce")
df = df.dropna(subset=["Amount"])
df = df[df["Amount"] != 0]
# Bepaal het eerste significante cijfer (strip valuta/duizendtallen en leidende nullen)
def first_sig_digit(x):
cleaned = re.sub(r"[^\d]", "", f"{abs(x):f}")
cleaned = cleaned.lstrip("0")
return int(cleaned[0]) if cleaned else np.nan
df["FirstDigit"] = df["Amount"].apply(first_sig_digit)
df = df.dropna(subset=["FirstDigit"])
df["FirstDigit"] = df["FirstDigit"].astype(int)
Werkelijke en verwachte verdeling vergelijken
Nu berekenen we hoe vaak elk eerste cijfer daadwerkelijk voorkomt in de declaraties en vergelijken dat met de Benford-verwachting.
actual = df["FirstDigit"].value_counts(normalize=True).sort_index() * 100
benford = pd.Series(
[30.1, 17.6, 12.5, 9.7, 7.9, 6.7, 5.8, 5.1, 4.6],
index=range(1, 10)
)
Visualisatie
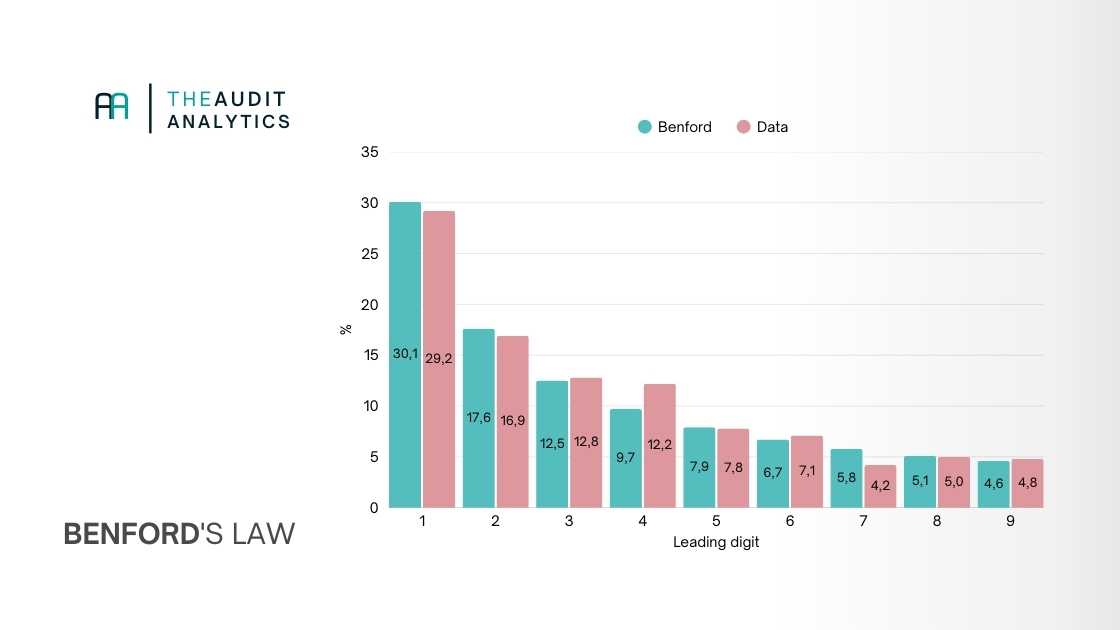
De grafiek hieronder laat in één oogopslag zien of het declaratiepatroon overeenkomt met Benford's Law. Grote verschillen kunnen duiden op afrondingsgedrag, bewust gekozen bedragen, of structurele afwijkingen.
plt.figure(figsize=(10, 6))
plt.bar(benford.index - 0.15, benford.values, width=0.3, label="Benford (verwacht)")
plt.bar(actual.index + 0.15, actual.values, width=0.3, label="Dataset (werkelijk)")
plt.title("Benford's Law - vergelijking van werkelijke verdeling met verwachting")
plt.xlabel("Eerste cijfer")
plt.ylabel("Percentage")
plt.grid(axis="y", linestyle="--", alpha=0.6)
plt.legend()
plt.tight_layout()
plt.show()
Dat ziet er dan uiteindelijk bijvoorbeeld zo uit:
Toetsen: is er echt een afwijking?
Een visuele vergelijking tussen de dataset en Benford's Law geeft een eerste indruk, maar is onvoldoende om te bepalen of een afwijking écht betekenisvol is. Kleine verschillen kunnen er op een grafiek groot uitzien, en subtiele patronen vallen soms juist niet op. Daarom gebruik je een formele toets om de afwijking te kwantificeren en te bepalen of het patroon binnen normale variatie valt.
Mean Absolute Deviation (MAD)
De MAD is de meest gebruikte maatstaf in forensische Benford-analyses. De toets berekent de gemiddelde absolute afwijking tussen de werkelijke verdeling en de Benford-verwachting.
Richtwaarden volgens Nigrini:
< 0.006 ? conform Benford
0.006-0.012 ? mogelijk afwijkend
> 0.012 ? duidelijk afwijkend
De MAD is robuust en vooral eenvoudig te berekenen. Daardoor is het laagdrempelig en goed te gebruiken in de audit. Het geeft je een indicatie; wat precies de bedoeling is bij het gebruik van Benford's Law in de audit.
Andere toetsen
Naast de MAD kun je, als je meer statistische zekerheid wilt, ook toetsen zoals de chi-kwadraattoets of de Kolmogorov' Smirnovtest gebruiken. Deze meten de totale afwijking van de verdeling, maar kunnen door grote aantallen observaties snel 'significant' worden.
Voorbeeld
Hieronder vind je een voorbeeld hoe je de MAD-test kunt berekenen met python.
import numpy as np
import pandas as pd
# Benford verwachte distributie
benford = pd.Series(
[30.1, 17.6, 12.5, 9.7, 7.9, 6.7, 5.8, 5.1, 4.6],
index=range(1, 10)
) / 100
# Werkelijke verdeling 'actual' uit eerdere stappen (als percentages)
actual = actual / 100 # omzetten naar fracties
# MAD-berekening
mad = (actual - benford).abs().mean()
mad
Stel dat de MAD-toets op de declaraties van medewerkers een score van 0.0148 oplevert. Dat ligt boven de grens van 0.012 en valt daarmee in de categorie 'afwijkend'.
Dit geeft dus geen bewijs dat er wel of geen fraude in zit (fraudeers die de wet kennen, kunnen hier ook rekening mee houden), maar het geeft wel aan waar je mogelijk extra aandacht op moet hebben.


